Dear Lovely Readers,
I've been writing this blog for 6 months now and am so excited at how useful it has been for so many of you. Thank you all for the feedback you have been giving me, it is truly appreciated.
As I have written the Blog, so my ideas have changed and developed and it is time for me to spend some time planning, and reviewing what I am doing and stop publishing articles for a while. Hopefully, when I relaunch it will be with a fully loaded website with ideas, resources and my weekly activities.
In order to do this, and still manage life with two small children, I am going to take a break from publishing anything on the blog until the end of the year.
In the meantime, your children have chance to get back into the routines of school and get their brains back into the habits of work everyday. If you have any thought / ideas / feedback for me, that I can then hopefully incorporate into my changes, I would love to hear from you. I am particularly interested to hear if there are any maths phrases and expressions that your children are coming home with that you need help interpreting :)
For those that would still like to be doing something at home with their children then keep counting, keep looking at mathematical things around you and talking about them. Most importantly, whatever you do, make it fun :)
Please email me your thoughts at cal@lotty.org
Have you ever found yourself wondering how you can help your child / children with their maths work? Whether it is to boost their skills, to increase their confidence or to challenge them further? As a Primary / Elementary School Maths Specialist my aim with this blog is to give parents guidance and ideas on how to do this. Alongside the ideas you will find explanations and examples of my experiences within the classroom to support my thinking and ideas and help develop your understanding.
Times Tables
For many here in the US, this week has been the first back at school and I know next week will be the start back for most of the UK. Therefore, I am expecting that most of you are going to have some pretty tired children as they readjust their body clocks back to school hours. What you will also find is that your children will all be searching hard through their brains to recall even the simplest of maths facts as a lots of these have been 'forgotten' over the long break.
Consequently, I thought we would start the academic year with some revision of basic maths facts: those facts that we all want to know but dread the learning process of, as most of us assume learning maths facts is one of the most boring things we can do!
So, time to dig through those memories and see how many times tables you can remember. Then you and your child can work together to revise what they 'should' know and then add a few more to the memory.
If you have been following my blog you will have already read an article I wrote, back in June, on learning times tables and this week I am just going to link you straight back to this article. For those that read and did some of the activities it is the perfect time to revisit this and revise what you did so please don't worry about repeating old stuff. Maths is often all about repeating, revising and improving knowledge each time.
'Number Sequences'. This details exactly how I teach times tables or number sequences, as some people call them. It is as fun as I can make it. I feel the worst thing about learning times tables is the way they are often taught - it's boring and uninspiring. What we actually need to do is inspire these children with this basic knowledge and make them want to learn more.
For those that want a little more fun, I read a blog post this week, written by a Mum that also finds learning times tables boring and has discovered a great way to learn them and have fun with them. Time to tune up those voices :)
https://www.scarymommy.com/the-math-trick-every-kid-should-know/
Have fun!
Symmetry
As we're getting to the end of the holidays for some and the beginning of the term for others I thought we would do another fun activity this week, without the pressure of trying to deal with numbers. I would imagine that those that are back at school are feeling a little fuzzy headed by the time they come home this week and therefore in need of something that can be fun as well as educational.

So, symmetry! This is a topic that I love to teach as you can get very creative with it and have huge amounts of fun. However, there is not always time to do the fun stuff. Unfortunately the fun bit is generally the consolidation bit so this topic does not always get fully understood at school. Often the children don't realise this as they can do the obvious symmetrical activities but it's the tricky bits that always catch them out.
Below I have described some activities that you can do with your children to really consolidate their knowledge of symmetry and to have some fun. These can all be adapted to suit the level your child is working at.
Symmetry Walk
Go for a walk around your neighbourhood or local shopping centre and find as many symmetrical things as you can. Each time one of you finds something, stop and discuss whether it is symmetrical or not. As parent you could find a couple of things that initially look symmetrical but upon discussion and closer inspection are not.
Photo Collage
Go for a walk or send your child to wonder the house and garden with a camera and ask him / her to take photographs of anything they find that is symmetrical. Once they have a specified number of photos (you will need to limit this or you will be discussing 50+ photos!) print them out (on paper, nothing special) and discuss why the item in the photo is symmetrical or not. By printing these out you are also then able to use a mirror to help work out if something is symmetrical or not.
Painting
We must have all done a symmetrical butterfly painting at some point in our lives. Here's the chance to do it again. There is the basic level butterfly of splosh some paint on half a piece of paper, fold the paper in half and press down. Unfold and 'hey presto' a butterfly has appeared. This can be extended by your child painting a specific pattern on one side and then letting it 'copy' onto the other. Another way of extending this is to get your child to paint a detailed symmetric butterfly by painting both sides and then folding it in half to check how symmetrical it really is.

Cutting and Pasting
Instead of paint you and your child could create a symmetrical picture. Fold a piece of paper in half (or quarters) and then stick onto the paper coloured bits of paper, sequins, pompoms etc. Make sure both sides (or all four sides) are symmetrical. You can make this a little more interesting by creating something specific eg a butterfly by folding the paper in half and cutting a butterfly shape out of it. Or a mask, a body, a specific shape like a square or a hexagon.
Mosaics
Depending on how messy you want to be you could do a mosaic with your child. This could be done with coloured pens on squared paper or by sticking on coloured squares. This activity is great for extending the older children as you can do diagonal lines of symmetry or 4 way symmetry.
Symmetry Table
Create a table on a large sheet of paper with two columns (possibly more depending on level). One column marked symmetrical and the other marked non-symmetrical. Or this could be marked with 1 line of symmetry, 2 lines of symmetry etc. Over a period of a few days get your child to complete the table by drawing a picture of anything she finds that would fit onto either column so eventually she / he should have up to 10 items in each column.

Symmetry pictures
Depending on your personal drawing skills you could draw half of various objects and get your child to draw the other half, keeping it symmetrical. For example you could draw half a ladybird and then pass it over for your child to draw the other half and colour it in (you may have already coloured your half in an interesting pattern ready to be copied. Children often love this as it's sitting and colouring. You could make it more fun by both of you drawing a half object and then exchanging.
Hopefully you are now inspired with lots of things to do but are maybe unsure of what level to do this out so here is a progress chart for symmetry. I have avoided using ages this time as this is not necessarily age dependent, some children can progress along this quite quickly given lots of practice.
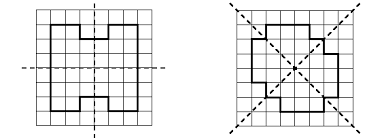
So, symmetry! This is a topic that I love to teach as you can get very creative with it and have huge amounts of fun. However, there is not always time to do the fun stuff. Unfortunately the fun bit is generally the consolidation bit so this topic does not always get fully understood at school. Often the children don't realise this as they can do the obvious symmetrical activities but it's the tricky bits that always catch them out.
Below I have described some activities that you can do with your children to really consolidate their knowledge of symmetry and to have some fun. These can all be adapted to suit the level your child is working at.
Symmetry Walk
Go for a walk around your neighbourhood or local shopping centre and find as many symmetrical things as you can. Each time one of you finds something, stop and discuss whether it is symmetrical or not. As parent you could find a couple of things that initially look symmetrical but upon discussion and closer inspection are not.
Photo Collage
Go for a walk or send your child to wonder the house and garden with a camera and ask him / her to take photographs of anything they find that is symmetrical. Once they have a specified number of photos (you will need to limit this or you will be discussing 50+ photos!) print them out (on paper, nothing special) and discuss why the item in the photo is symmetrical or not. By printing these out you are also then able to use a mirror to help work out if something is symmetrical or not.
Painting
We must have all done a symmetrical butterfly painting at some point in our lives. Here's the chance to do it again. There is the basic level butterfly of splosh some paint on half a piece of paper, fold the paper in half and press down. Unfold and 'hey presto' a butterfly has appeared. This can be extended by your child painting a specific pattern on one side and then letting it 'copy' onto the other. Another way of extending this is to get your child to paint a detailed symmetric butterfly by painting both sides and then folding it in half to check how symmetrical it really is.
Cutting and Pasting
Instead of paint you and your child could create a symmetrical picture. Fold a piece of paper in half (or quarters) and then stick onto the paper coloured bits of paper, sequins, pompoms etc. Make sure both sides (or all four sides) are symmetrical. You can make this a little more interesting by creating something specific eg a butterfly by folding the paper in half and cutting a butterfly shape out of it. Or a mask, a body, a specific shape like a square or a hexagon.
Mosaics
Depending on how messy you want to be you could do a mosaic with your child. This could be done with coloured pens on squared paper or by sticking on coloured squares. This activity is great for extending the older children as you can do diagonal lines of symmetry or 4 way symmetry.
Symmetry Table
Create a table on a large sheet of paper with two columns (possibly more depending on level). One column marked symmetrical and the other marked non-symmetrical. Or this could be marked with 1 line of symmetry, 2 lines of symmetry etc. Over a period of a few days get your child to complete the table by drawing a picture of anything she finds that would fit onto either column so eventually she / he should have up to 10 items in each column.
Symmetry pictures
Depending on your personal drawing skills you could draw half of various objects and get your child to draw the other half, keeping it symmetrical. For example you could draw half a ladybird and then pass it over for your child to draw the other half and colour it in (you may have already coloured your half in an interesting pattern ready to be copied. Children often love this as it's sitting and colouring. You could make it more fun by both of you drawing a half object and then exchanging.
Hopefully you are now inspired with lots of things to do but are maybe unsure of what level to do this out so here is a progress chart for symmetry. I have avoided using ages this time as this is not necessarily age dependent, some children can progress along this quite quickly given lots of practice.
- First step is to recognise simple shapes that are symmetrical and be able to mark on the line of symmetry. Eg draw a line of symmetry through a square or a triangle and then to venture slightly further and be able to draw one through a teddy bear picture or a picture of a spider etc.
- Once they can recognise this symmetry can your child draw it? If you drew half a square and the line of symmetry could they draw the other half - the reflection? Try it with a teddy bear.
- Once basic symmetry has been established you need to start putting this into context by looking at regular shapes and identifying how many lines of symmetry a shape has and where they are.
- Alongside the above children need to be able to draw what I would call a more random reflection. ie. They have a shape and a need to be able to reflect this in a line of symmetry that is not part of the shape.
- Once they can reflect a shape in one line of symmetry can they reflect it in a diagonal line of symmetry and then across 2 lines of symmetry? eg. Imagine a hexagon with a line of symmetry drawn vertically to it and then draw a line of symmetry across the bottom so it is horizontal to it - can they draw a reflection in both these lines?
I hope you all enjoy this weeks activity - something fun but educational :)
If anyone would like to help me I would love a little feedback from you all so I can make sure I am giving you the help and inspiration needed.. Nothing detailed but I would really appreciate it if you could email me (cal@lotty.org) or comment below and let me know your favourite article or top three articles. If you would like to give reasons for these that would be an added bonus for me. Thank you
Planes, trains and automobiles........
This week I thought I would give you a fun maths craft after the last few busy posts with lots of 'lesson' style learning. This also serves a double purpose as it gives you chance to revise the work some of you might have done on sequences a few weeks ago.
What you will need
A printed out train with many carriages or something else that has many of something!
This could be many aeroplanes, cars, beads, pictures of animals.........
(The one I used is here, you could do much bigger ones too)
Colouring pencils or pens
A sequence!
What to do
Choose a sequence with your child that they would like to learn / practice or revise.
With your child write the sequence on your train carriages (or something else)
Let your child colour in and or decorate their train.
Display your train (or other) on the wall. The more your child looks at it the more the sequence will sink in.
I know many children that would love this activity: a little bit of learning and then some colouring and decorating :)
Pre-school
These sequences will be the basics of numbers and you may need to start nice and easy with just the
Basic counting up as far as you can go
Counting backwards from 10 and then maybe 20
Counting in 2's to 20
Counting in 10's to 100
5, 6 and 7 year olds
These children will , hopefully, be confident counters by now but will need to be working on counting in sequences that miss out numbers, so 2's, 3's etc. The other area you may need to practice is going over 100.
Counting forwards - always worth practicing
Counting backwards - from any number below 100
Counting in 2's - as far as they can
Counting in 2's - but odd numbers
Counting in 5's - can they get to 50 or 100?
Counting in 10's - how far can they get?
Counting in 3's - up to 36 initially
Counting in 4's - up to 48 initially
7, 8 and 9 year olds
Hopefully most of these children have mastered the art of counting and can do the basic times table sequences. So the next challenge for these is to push them to know all their tables and to look slightly further afield.
Counting forwards - always worth practicing
Counting backwards - from any number below 300
Counting in 2's - as far as they can
Counting in 2's - but odd numbers
Counting in 5's - can they get beyond 100?
Counting in 10's - how far can they get?
Counting in 3's - up to 36 initially
Counting in 4's - up to 48 initially
Counting in 6's - up to 72 initially
Counting in 7's - up to 84 initially
Counting in 8's - up to 96 initially
Counting in 9's - up to 108 initially
Counting in 11's - up to 132 initially
Counting in 12's - up to 144 initially
9, 10 and 11 year olds
By now these children should be revising their times tables and pushing onto more interesting sequences:
Counting forwards - always worth practicing
Counting backwards - from any number
Counting in 2's - as far as they can
Counting in 2's - but odd numbers
Counting in 5's - can they get beyond 100?
Counting in 10's - how far can they get?
Counting in 3's - how far can they get?
Counting in 4's - how far can they get?
Counting in 6's - how far can they get?
Counting in 7's - how far can they get?
Counting in 8's - how far can they get?
Counting in 9's - how far can they get?
Counting in 11's - how far can they get?
Counting in 12's - how far can they get?
Can they start counting in any of the numbers above but starting from a different starting number eg. count in 6's starting on 2.
Counting in 13's
Counting in 15's
Counting in 25's
Counting in square numbers
Counting in triangular numbers
What other interesting sequences can you find? fibonacci, prime numbers, to the power of 2............
What you will need
A printed out train with many carriages or something else that has many of something!
This could be many aeroplanes, cars, beads, pictures of animals.........
(The one I used is here, you could do much bigger ones too)
Colouring pencils or pens
A sequence!
What to do
Choose a sequence with your child that they would like to learn / practice or revise.
With your child write the sequence on your train carriages (or something else)
Let your child colour in and or decorate their train.
Display your train (or other) on the wall. The more your child looks at it the more the sequence will sink in.
I know many children that would love this activity: a little bit of learning and then some colouring and decorating :)
Pre-school
These sequences will be the basics of numbers and you may need to start nice and easy with just the
Basic counting up as far as you can go
Counting backwards from 10 and then maybe 20
Counting in 2's to 20
Counting in 10's to 100
5, 6 and 7 year olds
These children will , hopefully, be confident counters by now but will need to be working on counting in sequences that miss out numbers, so 2's, 3's etc. The other area you may need to practice is going over 100.
Counting forwards - always worth practicing
Counting backwards - from any number below 100
Counting in 2's - as far as they can
Counting in 2's - but odd numbers
Counting in 5's - can they get to 50 or 100?
Counting in 10's - how far can they get?
Counting in 3's - up to 36 initially
Counting in 4's - up to 48 initially
7, 8 and 9 year olds
Hopefully most of these children have mastered the art of counting and can do the basic times table sequences. So the next challenge for these is to push them to know all their tables and to look slightly further afield.
Counting forwards - always worth practicing
Counting backwards - from any number below 300
Counting in 2's - as far as they can
Counting in 2's - but odd numbers
Counting in 5's - can they get beyond 100?
Counting in 10's - how far can they get?
Counting in 3's - up to 36 initially
Counting in 4's - up to 48 initially
Counting in 6's - up to 72 initially
Counting in 7's - up to 84 initially
Counting in 8's - up to 96 initially
Counting in 9's - up to 108 initially
Counting in 11's - up to 132 initially
Counting in 12's - up to 144 initially
9, 10 and 11 year olds
By now these children should be revising their times tables and pushing onto more interesting sequences:
Counting forwards - always worth practicing
Counting backwards - from any number
Counting in 2's - as far as they can
Counting in 2's - but odd numbers
Counting in 5's - can they get beyond 100?
Counting in 10's - how far can they get?
Counting in 3's - how far can they get?
Counting in 4's - how far can they get?
Counting in 6's - how far can they get?
Counting in 7's - how far can they get?
Counting in 8's - how far can they get?
Counting in 9's - how far can they get?
Counting in 11's - how far can they get?
Counting in 12's - how far can they get?
Can they start counting in any of the numbers above but starting from a different starting number eg. count in 6's starting on 2.
Counting in 13's
Counting in 15's
Counting in 25's
Counting in square numbers
Counting in triangular numbers
What other interesting sequences can you find? fibonacci, prime numbers, to the power of 2............
Have fun with this one!
Addition.......how do we teach it now?!!!
So, how do you help your child when it comes to addition?

Throughout their time at school your child will be exposed to many different methods of doing addition. Some will be written methods and others will be what we call mental methods - worked out in your head or using jottings. As a parent the best way you can help your child with their addition is to build up their ability to do addition in their heads - what I would call mental addition.
This will build your child's understanding of addition in a much better way than through using pencil and paper methods. To be able to do maths in your head you have to be able to understand what you are doing. Doing the mental methods will really build your child's knowledge and understanding of numbers. The danger with using pencil and paper methods is that your child doesn't fully understand what they are doing and can't do it in their heads and so ends up relying on a method they don't quite understand and therefore does not have the knowledge to recognise if they have gone wrong. I have seen it many times when children are working through sums. They bring me them to mark and several are obviously wrong if you look at the numbers but these children, because they are relying on the method, are not actually looking at the numbers. They are just putting them through a formula and not even looking at or thinking about what is coming out the other end so can't spot their mistakes. Giving your child a really secure mental knowledge and understanding is the best thing you can do for them.
So, now you know what to do here's how to do it.
As with everything start easy and build up. Easy builds the confidence.
When doing addition, your ultimate aim is for it to be done in the head or with simple jottings but you need to teach your child what to do in their head first. So, when doing the activities below you need to have something to write on so all practise can be done modelling what is going to be going on in the head and then, as time goes on, you can gradually take away how much is written down.

Level: Single digit addition progressing to 2-digit add 1-digit numbers
Find an object that you have many of! This could be crayons, books, duplos, cars............
Create a sum on the floor with your objects ie two small piles of cars. With your small child ask them how many cars there are and then how many cars there are in total and count them out together. One thing that is really good to do is to count the individual piles and then count the cars altogether and then start with one pile and say something similar to this:
'OK, I have 4 cars on this pile and 2 on the other pile. If I add them together I can do it by starting with the first number and then adding on the second. I know I have 4, so I don't need to recount them, I just add on the next two. So, 4, 5, 6. I have 6 in total.' Basically you are demonstrating that you don't need to count all the cars every time.
Once you have done the sum then swap the sum round so instead of it being 4 cars add 2 cars make it 2 cars add 4 cars.
After doing these sums write them out or encourage your child to help write them out so they can start to see how we write sums out. I would always try and use something fun for the writing like a whiteboard, a window or chalk, just makes it more fun for your child.
Once you have established basic addition you need to ensure they are starting to understand that:
Level: 2 digit add 2-digit numbers
When it comes to adding two 2-digit numbers together you need to start encouraging your child in a very visual method so they can start to internalise this and use it within their heads.
I teach this by writing the sum across the page and then drawing a loop on top of the sum from one units number to the other, adding them in my head and writing the total above the loop. Initially I write the sum above the loop too. Then I draw a loop under the sum from one tens number to the other and then, write the total of these under the loop. Again I start by writing the sum. Please, please write the full tens number of 20 or 30 etc. please don't just write 2 or 3 to show the number of tens. They really need the visual of the full tens number to help internalise that understanding. Once I have added the units and then the tens (please always try to demonstrate by doing the units first) I then write after the sum a new sum of the tens add the units with the answer. This is very visual and can really help your child to see and understand the process they need to go through to add numbers together. Although I encourage children to add the units first (this will help them with bigger numbers and when holding numbers in their heads) when they write the new sum I encourage them to write the hundreds number first, then the tens and then the units as this can help them see the numbers fit / add together.
6 + 3 = 9

eg. 26 + 13 = 30 + 9 =39

20 + 10 = 30
Once you have shown this method you will need to stay visual for a while but as your child increases in confidence and ability the next step is to slowly take away the visual and encourage them to do this within their heads.
1. Stop writing the sums on the loops, just write the answers
2. Next step is to take away the end sum where you add the tens and units, encourage them to do that sum in their heads and just write the answer.
3. Then the loops need to be dropped. As these are dropped you may want to use the final sum again, as a way of recording the answers to the mini sums eg.
26 + 13 = 30 + 9 = 39
Obviously the final step is then to drop that final sum and for all those steps to be done in the head.
The above process is not quick, it will take a lot of time and practice but eventually your child will get there and will have a fab understanding of numbers.
What you may find happens, is that every time you increase the level of the sum you will need to re-use some of the stepping stones above just to re internalise but also give your child the tools and time to learn to cope with bigger numbers.
Level: 3-digit numbers add 2- digit numbers
For these sums you need to use exactly the same visual as above. All you are doing is adding in a simple 100's element. You should still have 2 loops but when you write out the second sum you will have hundreds in there too. eg.
147 + 83 = 100 + 120 + 10 = 230
This is going to require lots of practice as there are many areas that can confuse a budding mathematician.
eg. 147 + 83 = 100 + 120 +10 = 200 + 30 = 230
Level: 3-digit numbers add 3-digit numbers
As with above you need to take this step by step and steadily.
Use the same method as above but this time you will need to add a third loop to add the hundreds numbers together. Likewise, add in the loop, do lots of practice and then slowly take the visual elements away until your child can add these numbers confidently in their heads.
Level: Bigger numbers!
I could go on describing the gradual increase with 3-digit add 4-digt etc. but I think you should understand what you are doing by now. Your child should also understand. If the previous levels have been taught slowly and steadily then by the time you hit 4-digit numbers your child should be able to manage very easily in his / her head without having to go through the written / visual process to practice.
The basics you need for teaching mental addition is paper and pencil and some objects if you have a young mathematician.
As with many aspects of maths this part of maths does initially require some sitting down and learning but we can make it more fun and interesting
Dice - use these to create your sums. Each dice throw represents another digit in the sum (yes, the dice only go to 6 but this can work great when moving up a levle as it keeps the sums a little simpler)
Number cards - your child may love making some numbers cards 0 - 9 which you can then use to help you pick the numbers for your sums
Race - children love racing / working against an adult. Write a sum and both of you race to do it
Taking it in turns - write sums for each other. So you write one for your child to do, they write one for you to do. (establish rules for the sums if you do this ie. 2 digit numbers etc.)
Timer - this can be used in several ways: how many sums in 1 minute or you could set a target of 'can you do 3 sums in one minute.
Obviously there is lots of progression that can be made with this topic. My advice is to find your childs level and with that to improve it a little and then do lots of practice around it. Then in a few weeks come back to it and move them on again. Go slowly and steadily. There is no rush. The most important thing here is that you are developing a clear understanding of addition in your child.
Once you have done the sitting down teacher bit you need to practice. Again, this can be done in may ways.
Sitting down practice - every few days sitting together and working through some sums
Random - every so often just ask your child what the answer to a sum is eg. What's 7 + 26 . This can be quite fun if you just add it into your everyday life.
Hide and seek numbers - hide some numbers (these need to be full numbers at the level you're working at) around a room / the house. Get your child to find 2 and add them together. Hide them again and then they need to find another 2 and add them.
Bribery games - some children may need more of an incentive and you could score points for every sum they get right doing the activities suggested above. When they have so many points they could earn something. Generally with my daughter when she earns something it's craft time with me or a day out of her choice (within budget) etc.


Throughout their time at school your child will be exposed to many different methods of doing addition. Some will be written methods and others will be what we call mental methods - worked out in your head or using jottings. As a parent the best way you can help your child with their addition is to build up their ability to do addition in their heads - what I would call mental addition.
This will build your child's understanding of addition in a much better way than through using pencil and paper methods. To be able to do maths in your head you have to be able to understand what you are doing. Doing the mental methods will really build your child's knowledge and understanding of numbers. The danger with using pencil and paper methods is that your child doesn't fully understand what they are doing and can't do it in their heads and so ends up relying on a method they don't quite understand and therefore does not have the knowledge to recognise if they have gone wrong. I have seen it many times when children are working through sums. They bring me them to mark and several are obviously wrong if you look at the numbers but these children, because they are relying on the method, are not actually looking at the numbers. They are just putting them through a formula and not even looking at or thinking about what is coming out the other end so can't spot their mistakes. Giving your child a really secure mental knowledge and understanding is the best thing you can do for them.
So, now you know what to do here's how to do it.
As with everything start easy and build up. Easy builds the confidence.
When doing addition, your ultimate aim is for it to be done in the head or with simple jottings but you need to teach your child what to do in their head first. So, when doing the activities below you need to have something to write on so all practise can be done modelling what is going to be going on in the head and then, as time goes on, you can gradually take away how much is written down.
How to teach mental addition
Level: Single digit addition progressing to 2-digit add 1-digit numbers
Find an object that you have many of! This could be crayons, books, duplos, cars............
Create a sum on the floor with your objects ie two small piles of cars. With your small child ask them how many cars there are and then how many cars there are in total and count them out together. One thing that is really good to do is to count the individual piles and then count the cars altogether and then start with one pile and say something similar to this:
'OK, I have 4 cars on this pile and 2 on the other pile. If I add them together I can do it by starting with the first number and then adding on the second. I know I have 4, so I don't need to recount them, I just add on the next two. So, 4, 5, 6. I have 6 in total.' Basically you are demonstrating that you don't need to count all the cars every time.
Once you have done the sum then swap the sum round so instead of it being 4 cars add 2 cars make it 2 cars add 4 cars.
After doing these sums write them out or encourage your child to help write them out so they can start to see how we write sums out. I would always try and use something fun for the writing like a whiteboard, a window or chalk, just makes it more fun for your child.
Really important - when writing out the sums for mental addition please always write them out horizontally, across the page
Once you have established basic addition you need to ensure they are starting to understand that:
- You don't have to count each time
- Addition sums can be done either way round and give the same answer
- Their fingers can help them - our number system is base 10 so having ten fingers works really well for addition
Level: 2 digit add 2-digit numbers
When it comes to adding two 2-digit numbers together you need to start encouraging your child in a very visual method so they can start to internalise this and use it within their heads.
I teach this by writing the sum across the page and then drawing a loop on top of the sum from one units number to the other, adding them in my head and writing the total above the loop. Initially I write the sum above the loop too. Then I draw a loop under the sum from one tens number to the other and then, write the total of these under the loop. Again I start by writing the sum. Please, please write the full tens number of 20 or 30 etc. please don't just write 2 or 3 to show the number of tens. They really need the visual of the full tens number to help internalise that understanding. Once I have added the units and then the tens (please always try to demonstrate by doing the units first) I then write after the sum a new sum of the tens add the units with the answer. This is very visual and can really help your child to see and understand the process they need to go through to add numbers together. Although I encourage children to add the units first (this will help them with bigger numbers and when holding numbers in their heads) when they write the new sum I encourage them to write the hundreds number first, then the tens and then the units as this can help them see the numbers fit / add together.
6 + 3 = 9
eg. 26 + 13 = 30 + 9 =39
20 + 10 = 30
Once you have shown this method you will need to stay visual for a while but as your child increases in confidence and ability the next step is to slowly take away the visual and encourage them to do this within their heads.
1. Stop writing the sums on the loops, just write the answers
2. Next step is to take away the end sum where you add the tens and units, encourage them to do that sum in their heads and just write the answer.
3. Then the loops need to be dropped. As these are dropped you may want to use the final sum again, as a way of recording the answers to the mini sums eg.
26 + 13 = 30 + 9 = 39
Obviously the final step is then to drop that final sum and for all those steps to be done in the head.
The above process is not quick, it will take a lot of time and practice but eventually your child will get there and will have a fab understanding of numbers.
What you may find happens, is that every time you increase the level of the sum you will need to re-use some of the stepping stones above just to re internalise but also give your child the tools and time to learn to cope with bigger numbers.
Level: 3-digit numbers add 2- digit numbers
For these sums you need to use exactly the same visual as above. All you are doing is adding in a simple 100's element. You should still have 2 loops but when you write out the second sum you will have hundreds in there too. eg.
147 + 83 = 100 + 120 + 10 = 230
This is going to require lots of practice as there are many areas that can confuse a budding mathematician.
- Suddenly they are dealing with three numbers
- They may have hundreds in more than one number in their second sum and tens in more than one number.....
- They have to go into much higher numbers
eg. 147 + 83 = 100 + 120 +10 = 200 + 30 = 230
Level: 3-digit numbers add 3-digit numbers
As with above you need to take this step by step and steadily.
Use the same method as above but this time you will need to add a third loop to add the hundreds numbers together. Likewise, add in the loop, do lots of practice and then slowly take the visual elements away until your child can add these numbers confidently in their heads.
Level: Bigger numbers!
I could go on describing the gradual increase with 3-digit add 4-digt etc. but I think you should understand what you are doing by now. Your child should also understand. If the previous levels have been taught slowly and steadily then by the time you hit 4-digit numbers your child should be able to manage very easily in his / her head without having to go through the written / visual process to practice.
Activities
The basics you need for teaching mental addition is paper and pencil and some objects if you have a young mathematician.
As with many aspects of maths this part of maths does initially require some sitting down and learning but we can make it more fun and interesting
Dice - use these to create your sums. Each dice throw represents another digit in the sum (yes, the dice only go to 6 but this can work great when moving up a levle as it keeps the sums a little simpler)
Number cards - your child may love making some numbers cards 0 - 9 which you can then use to help you pick the numbers for your sums
Race - children love racing / working against an adult. Write a sum and both of you race to do it
Taking it in turns - write sums for each other. So you write one for your child to do, they write one for you to do. (establish rules for the sums if you do this ie. 2 digit numbers etc.)
Timer - this can be used in several ways: how many sums in 1 minute or you could set a target of 'can you do 3 sums in one minute.
Obviously there is lots of progression that can be made with this topic. My advice is to find your childs level and with that to improve it a little and then do lots of practice around it. Then in a few weeks come back to it and move them on again. Go slowly and steadily. There is no rush. The most important thing here is that you are developing a clear understanding of addition in your child.
Once you have done the sitting down teacher bit you need to practice. Again, this can be done in may ways.
Sitting down practice - every few days sitting together and working through some sums
Random - every so often just ask your child what the answer to a sum is eg. What's 7 + 26 . This can be quite fun if you just add it into your everyday life.
Hide and seek numbers - hide some numbers (these need to be full numbers at the level you're working at) around a room / the house. Get your child to find 2 and add them together. Hide them again and then they need to find another 2 and add them.
Bribery games - some children may need more of an incentive and you could score points for every sum they get right doing the activities suggested above. When they have so many points they could earn something. Generally with my daughter when she earns something it's craft time with me or a day out of her choice (within budget) etc.
So, this week is a slightly different week in that it is more teaching a skill but it's a really useful skill to have and the number confidence it will give your child is well worth it. Enjoy :)
Problem Solving - where do I start?
Problem Solving - is this a phrase that you have heard many times in conjunction with your childs maths work but are actually unsure what it means?
I would imagine that you are not alone. In the good old days, where teaching was more traditional this phrase would generally mean giving children some pre-written word problems that were linked to some of the work they were doing. These were very staged and mostly unrealistic. However, these days problem solving means something entirely different and requires and a very different way of looking at maths.

Over the past few years maths teaching has developed and changed and there is now a strong belief of teaching for understanding. Basically we really want your children to understand what they are learning and how it works, rather than just to know a formula and how to put the numbers through it. Part of this teaching for understanding is problem solving. These days we want to teach children through problems and discussion. By doing this your child has to think about what they know and apply this to the problem and can often extend their own learning and what they know by working through a problem. Initially, this can be quite a difficult thing to understand and get our heads around, as parents. But once you start to get into it this can be great fun and a learning curve for all. The great thing about problem solving is it can be a learning adventure for everyone at any level.
There are a wide range of methods for using problem solving to teach. Children can solve collaboratively or independently. New ideas can be taught or old ones consolidated. Problems can extends a child's knowledge of a particular concept or just give them the vision to understand what they thought they knew.
I thought that today I would introduce problem solving to you as a parent / tutor and start showing you how this can be used to help your children.
As I mentioned above, problem solving is very open ended and, I believe, the part that we, older people, struggle with the most is the fact there are no answers! We were brought up on the concept of maths being right and wrong. Problem solving is all about exploring and experimenting with numbers, a very different way of looking at things.
So, here is today's activity.

This is an incredibly open ended problem which makes it a fab problem as there is so much that can be done with it but also one where lots of encouragement could be needed as it's quite easy to be lazy on this problem.
When it comes to doing this problem with your child you may be lucky and have a child that is used to this kind of thing and will just get stuck in and play with those numbers. I would expect though, that most of you will have children that will look at you blankly and not know how to start. Below I have given you some question that will hopefully get the problem started and then just go from there. You will need paper and pens for all the jottings you might do.
When you introduce this problem keep it very simple and try not to give too much info and see what your child does. If they are not sure how to start, use some of the questions to help. The idea behind the questions is that they will spark other ideas and thoughts and hopefully you and your child, together, will start to explore the numbers without the aide of my questions. The questions are there purely to get you going enough to get the ideas and conversation flowing with these numbers. I have only given questions and not broken this down into levels this week as it is so open ended. Go with the flow, start with the very simple questions whatever level your child and just keep nudging the conversation deeper and deeper depending on what level your child is. I have added in some more difficult question to really push that thinking if some children are struggling to do this on their own.
Number
What's the biggest number you can make using all of these digits?
What's the smallest number you can make using these digits?
Counting
Can you count with them?
Can you count forwards? backwards?
Can you count every other number? What are those numbers? What about the ones you missed out?
Can you join one of the numbers to each of the other numbers and make a sequence? What sequence did you make? Can you count further than you made?
Adding
Can you add any of the numbers together?
Can you add the first number to each of the other numbers? What happens to them? What about if you add the second number to each of the others? the third? etc.?
Can you add all the numbers together?
What happens if you add 1, 2 and 3 together? Now add 2, 3 and 4, what do you get? What about 3, 4 and 5? Continue.........look at all the answers.
Can you add any of these numbers together to make 10? Do any of the other numbers add together to make 10? How many different ways can you make 10? What about doing the same for 11, 12 etc.
Subtracting
Can you start at 9 and take each of the the numbers before it away? eg 9 - 8 - 7 - 6.......... (you may get 'no you can't' or you may get 'yes' and be able to start exploring the negative numbers they go into - particularly good with 9, 10 and 11 year olds)
Which numbers can you pair up so that you can take one away from the other and stay with positive numbers?
Can you take more than one of the numbers away from any of the numbers? What's the highest numbers of these numbers that you can take away from one of these numbers?
Multiplying
Can you multiply any of these numbers together?
What happens if you multiply the numbers all by the last number: zero?
Can you multiply more than 2 of these numbers together?
Can you multiply all these numbers together?
What happens if you multiply all the numbers by one of the numbers? Now do this again with another of the numbers?
Can you multiply the numbers together in groups of three? Are there any patterns? What about if you multiply them together in groups of 4?
Dividing
Can you divide any of these numbers by one of the other numbers? Which ones? Did you develop a system to help you work this out methodically? If not, would this help?
Can you find a number that all of these numbers divide by? Can you find a number that none of these numbers divide by?
Can you put all the numbers together except one. The ones that are together should make a number that divide by the one not included (eg. 123467890 divided by 5)
Playing
Can you find another way to explore / play with these numbers?
Have fun and enjoy this weeks problem. I would love to hear about some of the discussions you have with this problem and how far into number exploration it took you.
I would imagine that you are not alone. In the good old days, where teaching was more traditional this phrase would generally mean giving children some pre-written word problems that were linked to some of the work they were doing. These were very staged and mostly unrealistic. However, these days problem solving means something entirely different and requires and a very different way of looking at maths.
Over the past few years maths teaching has developed and changed and there is now a strong belief of teaching for understanding. Basically we really want your children to understand what they are learning and how it works, rather than just to know a formula and how to put the numbers through it. Part of this teaching for understanding is problem solving. These days we want to teach children through problems and discussion. By doing this your child has to think about what they know and apply this to the problem and can often extend their own learning and what they know by working through a problem. Initially, this can be quite a difficult thing to understand and get our heads around, as parents. But once you start to get into it this can be great fun and a learning curve for all. The great thing about problem solving is it can be a learning adventure for everyone at any level.
There are a wide range of methods for using problem solving to teach. Children can solve collaboratively or independently. New ideas can be taught or old ones consolidated. Problems can extends a child's knowledge of a particular concept or just give them the vision to understand what they thought they knew.
I thought that today I would introduce problem solving to you as a parent / tutor and start showing you how this can be used to help your children.
As I mentioned above, problem solving is very open ended and, I believe, the part that we, older people, struggle with the most is the fact there are no answers! We were brought up on the concept of maths being right and wrong. Problem solving is all about exploring and experimenting with numbers, a very different way of looking at things.
So, here is today's activity.
Explore the numbers: 1, 2, 3, 4, 5, 6, 7, 8, 9 and 0.
This is an incredibly open ended problem which makes it a fab problem as there is so much that can be done with it but also one where lots of encouragement could be needed as it's quite easy to be lazy on this problem.
When it comes to doing this problem with your child you may be lucky and have a child that is used to this kind of thing and will just get stuck in and play with those numbers. I would expect though, that most of you will have children that will look at you blankly and not know how to start. Below I have given you some question that will hopefully get the problem started and then just go from there. You will need paper and pens for all the jottings you might do.
When you introduce this problem keep it very simple and try not to give too much info and see what your child does. If they are not sure how to start, use some of the questions to help. The idea behind the questions is that they will spark other ideas and thoughts and hopefully you and your child, together, will start to explore the numbers without the aide of my questions. The questions are there purely to get you going enough to get the ideas and conversation flowing with these numbers. I have only given questions and not broken this down into levels this week as it is so open ended. Go with the flow, start with the very simple questions whatever level your child and just keep nudging the conversation deeper and deeper depending on what level your child is. I have added in some more difficult question to really push that thinking if some children are struggling to do this on their own.
Number
What's the biggest number you can make using all of these digits?
What's the smallest number you can make using these digits?
Counting
Can you count with them?
Can you count forwards? backwards?
Can you count every other number? What are those numbers? What about the ones you missed out?
Can you join one of the numbers to each of the other numbers and make a sequence? What sequence did you make? Can you count further than you made?
Adding
Can you add any of the numbers together?
Can you add the first number to each of the other numbers? What happens to them? What about if you add the second number to each of the others? the third? etc.?
Can you add all the numbers together?
What happens if you add 1, 2 and 3 together? Now add 2, 3 and 4, what do you get? What about 3, 4 and 5? Continue.........look at all the answers.
Can you add any of these numbers together to make 10? Do any of the other numbers add together to make 10? How many different ways can you make 10? What about doing the same for 11, 12 etc.
Subtracting
Can you start at 9 and take each of the the numbers before it away? eg 9 - 8 - 7 - 6.......... (you may get 'no you can't' or you may get 'yes' and be able to start exploring the negative numbers they go into - particularly good with 9, 10 and 11 year olds)
Which numbers can you pair up so that you can take one away from the other and stay with positive numbers?
Can you take more than one of the numbers away from any of the numbers? What's the highest numbers of these numbers that you can take away from one of these numbers?
Multiplying
Can you multiply any of these numbers together?
What happens if you multiply the numbers all by the last number: zero?
Can you multiply more than 2 of these numbers together?
Can you multiply all these numbers together?
What happens if you multiply all the numbers by one of the numbers? Now do this again with another of the numbers?
Can you multiply the numbers together in groups of three? Are there any patterns? What about if you multiply them together in groups of 4?
Dividing
Can you divide any of these numbers by one of the other numbers? Which ones? Did you develop a system to help you work this out methodically? If not, would this help?
Can you find a number that all of these numbers divide by? Can you find a number that none of these numbers divide by?
Can you put all the numbers together except one. The ones that are together should make a number that divide by the one not included (eg. 123467890 divided by 5)
Playing
Can you find another way to explore / play with these numbers?
Have fun and enjoy this weeks problem. I would love to hear about some of the discussions you have with this problem and how far into number exploration it took you.
Subscribe to:
Posts (Atom)
